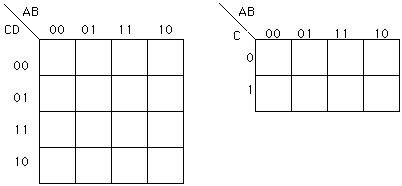
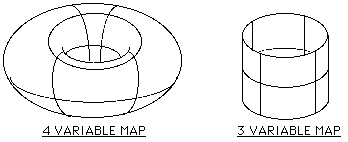
The maps above are organized so that groups like AB + AB' can be recognized and reduced (to A in this case) visually. To do this the truth table is mapped into the Karnaugh map and then squares of '1's are circled from the biggest square to the smallest square. It is important that the minimum number of circles is used and that the biggest possible squares is used in order to achieve a minimum reduction. When identifying squares, it must be kept in mind that the maps are actually three dimensional as shown below:

Example:

	The truth table on the right has been mapped into the KMap 
	and then the squares of '1 's circled. Notice that the number 
	of '1's in a square is always a power of 2.

	

	


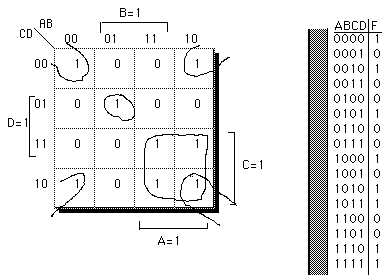
	Writing out the term for each group yields the expression below:

	F = A'BC'D + AC + B'D'

This page last modified: Friday, 21-Aug-2020 15:27:39 CST

Accessed     times.

CS Dept Home Page

CS Dept Class Files

CS400 Lab Outline