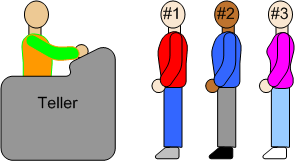
The main difference between a queue and a stack is that elements in a queue are put on the bottom and taken off the top (remember, in a stack, elements put on the top and taken off the top). For an everyday queue example, consider a line of customers at a bank waiting to be served. Each new customer gets in line at the rear. When the teller is ready to help a new customer, the customer at the front of the line is served. This is a queue--the first customer in line is the first one served.
A specific example of print queues follows:
| |
Removes all the elements from a queue | |
| |
Determines whether the queue is empty | |
| |
Determines whether the queue is full | |
| |
Adds an item to the rear of the queue | |
| |
Removes front item from the queue and returns it | |
| |
Outputs the elements of a queue |
Waiting is the critical element of queues. The objective of a queuing system is to utilize the servers (the tellers, CPU, operators, and so on) as fully as possible, while keeping the wait time within a reasonable limit.
So, in real life, how does a company determine the optimal compromise between the number of servers and the wait time? One way is through experience. The company tries out different numbers of servers and sees how things work out. There are two problems with this approach: 1) it takes too long, and 2) it is too expensive. A better approach is to use a computer simulation of the tellers, customers, and wait time. This approach uses queues.
Initialize the queue to empty.
for ( minute = 0 ; minute < n ; ++minute )
{
if the queue is not empty, then remove the customer at the front of the queue.
Compute a random number k between 0 and 3.
If k is 1, then add one customer to the line.
If k is 2, then add two customers to the line.
Otherwise (if k is 0 or 3), do not add any customers to the line.
}
In addition, the algorithm will keep track of the following:
| minute | queue isempty? |
k | queue operations | corresponding diagram |
|---|---|---|---|---|
| 0 | yes | no dequeue (empty queue) | ||
| 1 | enqueue(0) | |||
| 1 | no | |||
| dequeue | ||||
| 2 | enqueue(1) | |||
| enqueue(1) | ||||
| 2 | no | |||
| dequeue | ||||
| 2 | enqueue(2) | |||
| enqueue(2) | ||||
| 3 | no | |||
| dequeue | ||||
| 1 | enqueue(3) | |||
| 4 | no | |||
| dequeue | ||||
| 0 | no enqueue (k=0) |
Notice that the data in the node is the time (minute) that the "customer" joined the line. This data is used to compute the wait time of a customer.
The file: StoreSim.zip
This program consists of a "check-out line" simulation program (storesim.cpp), and a header file for implementing the Queue (queuelnk.h). In this exercise, the Queue is implemented as a linked list.
Your primary tasks for this exercise are the following:
As a general overview, add code to:
Test Plan for "Check-out Line" Simulation Program
| Time (minutes) | Total Number of Customers Served |
Average Wait | Longest Wait |
|---|---|---|---|
| 30 | |||
| 60 | |||
| 120 | |||
| 480 |
| |
|
|