CS210 Lab: Stack and Exception Handling
Highlights of This Lab:
Lab Exercise:

Click the little computer above for a detailed description.
For this excercise you will be asked to implement a stack
to recognize whether or not a set of parentheses
is well-formed.
1. Definition of a Stack
A Stack is "an abstract data type in which elements are added
and removed from only one end; a 'last in, first out' (LIFO) structure."
(C++ Plus Data Structures, page 196)
In a Stack implementation,
items are added to and removed from the top of the pile.
Consider the pile of papers on your desk.
Suppose you add papers only to the top of the pile or remove
them only from the top of the pile.
At any point, the only paper that is visible is the one on top.
What you have is a Stack.
1.1 Applications of a Stack
Here are a few examples of where stacks would be used:
- determining well-formed parenthesis.
For example: ((a+b)*c)
- calculating using RPN (Reverse Polish Notation).
For example:1 2 + 3 *
- keeping track of operation calls in programming language systems.
For example: The main program calls operation A,
which calls operation B, which calls operation C.
When C finishes, control returns to B;
when B finishes, control returns to A; and so on.
- analysing syntax for nested components (compiler use).
For example, for loops can contain
if-then
statements that contain
while loops.
As the compiler works through such nested constructs,
it "saves" information about what it is currently
working on in a stack.
When it finishes its work on the innermost construct,
the compiler can "retrieve" its previous status from
the stack, and pick up where it left off.
1.2 Typical Operations of a Stack
| |
- bool IsEmpty
|
Determines whether the stack is empty |
| |
- bool IsFull
|
Determines whether the stack is full |
| |
- Push(ItemType item)
|
Adds an item to the top of the stack |
| |
- Pop()
|
Removes top item from the stack |
| |
- ItemType Top()
|
Returns a copy of the top item on the stack |
2. Application: Determining Well-Formed Expressions with Parenthesis
The following section outlines an algorithm for determining whether or not an expression is well formed.
Later, in the lab exercise, you will be given a chance to play with and modify this program.
A classic use of a stack is for determining whether a set of parenthesis is
"well formed". What exactly do we mean by well formed?
In the case of parenthesis pairs, for an expression to be well formed, a
closing parenthesis symbol must match the last unmatched opening parenthesis
symbol and all parenthesis symbols must be matched when the input is finished.
Consider the following table demonstrating Well-Formed Versus Ill-Formed Expressions:
| Well-Formed Expressions |
Ill-Formed Expressions |
| ( x x x [ ] ) |
( x x x [ ) |
| ( ) [ ] { } |
( ( |
| { ( x x x x x ) ( ) } |
{ x x x x x ) ( ) } |
Why do we care about balancing parenthesis?
Because the compiler looks for balanced parenthesis in such situations as:
- nested components
(such as for loops, if-then statements,
and while loops).
The compiler checks for matching {} pairs to denote blocks of code.
If the pairs do not match, a compiler error will occur.
- mathmatical expressions. For example a = b - {(x + y) * z + 3};
- array notation [ ].
- function calls and function definitions. Specifically, the parameters must be surrounded by balanced "(" ")".
2.1 The Algorithm
Given an expression with characters and parenthesis, ( ), [ ], and { },
determine if an expression is well-formed by using the following algorithm in
conjunction with a stack.
Read in the expression character by character. As each character is read in:
- If the character is an opening symbol (characters "(", "{", or "["),
then push it onto the stack
- Else if the character is a closing symbol
(characters ")", "}", or "]"), then:
- Check if the stack is empty. If it is,
then there is no matching opening symbol.
The expression is not well formed.
- Else,
- get the character at the top of the stack
- pop the stack
- compare the current closing symbol to the
top symbol. If they balance each other, then
the expression is still balanced and continue
looping (reading the next character)
- If the end of the expression is reached, and it is still balanced,
then print "expression is well formed"
- Otherwise, print "expression is not well formed"
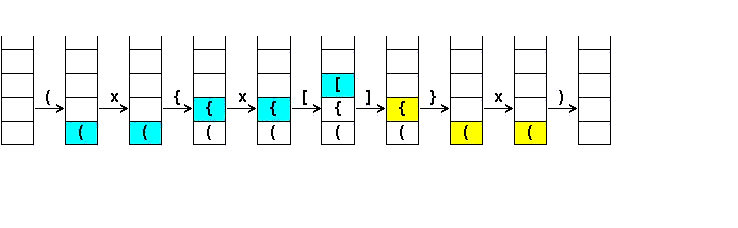
The expression:
(x{x[]}x)
yields the following computation
| '(' |
: Push ( |
| 'x' |
: Ignore |
| '{' |
: Push { |
| 'x' |
: Ignore |
| '[' |
: Push [ |
']'
|
: Get top of stack, openSymbol='['
Pop
Compare if '[' matches ']' |
'}'
|
: Get top of stack, openSymbol='{'
Pop
Compare if '{' matches '}' |
| 'x' |
: Ignore |
')'
|
: Get top of stack, openSymbol='('
Pop
Compare if '(' matches ')' |
| '\n' |
: Print expression is well-formed |
Or graphically:
3. Lab Exercise
Stacks and Exception Handling
- Get the files:
Click here
to get the zipped files for this exercise.
- Extract all of the files. Double
click on StackExercise.sln. This will open up the project.
There are four files used in this project:
- Balanced.cpp -- the main program.
You will modify the code in this file only.
- StackType.cpp and StackType.h --
the array implementation of the stack is from the
C++ Plus Data Structures textbook.
- ItemType.h -- contains the definitions of
MAX_ITEMS and ItemType.
Your primary tasks for this exercise are:
- Fix the bug which occurs when there are open parenthesis
but no corresponding closing parenthesis.
- Create exception handling so that no errors occur
when the stack is full.
Steps include:
-
Build an executable file.
-
Run the executable file, trying the test plan cases in the table below.
-
You should find a couple incorrect results as you try the test plan cases. This is becaue there were problems with the algorithm. Correct these problems one at a time:
- Program does not recognize that opening parenthesis without
matching closing paranthesis is NOT a well-formed expression.
For example, test case # 5: ( x ( x [ ] x.
To fix this problem, you will have to set balanced to false
if the stack is not empty at the end of the expression.
- Program exits with "Debug Error" message box.
For example, test case # 7: ( x ( ( ( ( ( (.
To fix this, you will have to use exception handling to
"catch" the "FullStack" exception.
For more on exception handling and
hints for fixing this problem click
here.
-
Once these problems are fixed, try the test plan cases once again and create some of your own.
Test Plan for the Balanced Parenthesis Evaluation Program
| # |
Parenthesis Expression |
Expected Result |
Checked |
| 1 |
() |
|
|
| 2 |
(( |
|
|
| 3 |
({[]}) |
|
|
| 4 |
([)] |
|
|
| 5 |
(([] |
|
|
| 6 |
()] |
|
|
| 7 |
(((((((( |
|
|
4. Postlab Exercises
For postlab exercices, click here.
 Copyright: Department of Computer Science, University of Regina.
Copyright: Department of Computer Science, University of Regina.
