CS201 Lab: Sequential Design
Objectives
- Review the Flip-Flops
- Examine the Sequential Design Procedure
- Build circuits to verify the suquential design procedures
A Note
We have worked on combinational design; that is the design of
circuits with no memory. This week we will start to look at
sequential design, which is the design of circuits with memory.
Sequential design will let us design much more complicated and
useful circuits like counters and even microprocessors.
Definition of Sequential Circuits
Sequential circuits are circuits that have memory.
In other words, these are circuits where the output depends on
the current inputs and the previous inputs.
In combinational circuits the output depends only on the current inputs.
Flip Flops
Flip-Flops are basic storage/memory elements. A sequential circuit consists of
a combinational circuit and storage elements (flip-flops) that together form a
feedback system. We cannot continue with anymore theory until we look at the
basic memory elements used in sequential design.
Some of the basic flip-flops are listed below:
- Set-Reset flip flop
The most basic flip flop is the S-R flip flop. (llustrate the
operation of the F/F using the diagram below ).

NOR is 1 iff all inputs are 0.
S=1 -> Q'=0, but then Q depends on R
S=1, R=1 -> Q = 0, Q' = 0, Undefined
R=0, S=1 -> Q = 1, Q' = 0. called "Set"
R=1, S=0 -> Q = 0, Q' = 1. called "Reset"
R=0, S=0 -> Q(t+1) = Q(t). called "Hold"
S R Q Q'
------------
0 0 1 0
1 0 1 0
------------
0 1 0 1
0 0 0 1
------------
1 1 0 0 Undefined
-------------------------
- Gated S-R flip flop
Quite often we only want the flip flop to be able to change states at certain times.
For example one may have a flip-flop in an alarm system that is set by a window
opening thus setting off the alarm. To prevent the alarm from going off when
the alarm system is shut off we would like to disable the flip-flop
when the alarm system is shut off. We can do this by adding some gates
to a S-R F/F to make it a gated S-R F/F.
(Illustrate the operation of the gated S-R F/F using the diagram below ).

In practice S-R F/Fs are not used that often. The most commonly used
flip-flops are the D-flip flop and the JK flip-flop. We will look at each
one in more details.
- D flip flop
The D flip-flop(shown below) lets the input at D propogate through to Q on
the positive going edge of the clock. The present state-next state chart
illustrates the behavior of the D flip-flop.
Basically Q(t+1) = D, which is the characteristic equation.
Characteristic Table Excitation Table
==================== ===================
D Q(t+1) Operation Q(t) Q(t+1) D
==================== ===================
0 0 Reset 0 0 0
-------------------- -------------------
1 1 Set 0 1 1
==================== -------------------
1 0 0
-------------------
1 1 1
===================

- JK flip-flop
The JK flip-flop(shown below) is very flexible and therefore allows simpler
circuit designs. Most JK flip-flops allow the signal to change on
the negative edge of the clock. The present state-next state
chart(shown below ) illustrates the behavior of the flip-flop.
The characteristic equation is Q(t+1) = JQ'(t) + K'Q(t).
Characteristic Table Excitation Table
========================== ===================
J K Q(t+1) Operation Q(t) Q(t+1) J K
========================== ===================
0 0 Q(t) No Change 0 0 0 x
-------------------------- -------------------
0 1 0 Reset 0 1 1 x
-------------------------- -------------------
1 0 1 Set 1 0 x 1
-------------------------- -------------------
1 1 Q'(t) Complement 1 1 x 0
========================== ===================

Sequential Design Procedure
1. State the problem clearly
2. Determine inputs/outputs and assign letters to inputs/outputs
Determine state bits and assign letters to the state bits
3. Draw a present state-next state diagram
4. Form the state table
5. For each input/output draw the karnaugh maps
6. Find the simplified expressions for the inputs/outputs using
Karnaugh maps
7. Draw the logic diagram and implement the circuit in LogicWorks
(a connection diagram will be needed if the circuit is to be hardwired)
Sequential Design Example
We have now covered the basic sequential circuit elements necessary
to construct sequential designs.
We will learn how to interconnect
JK flip-flops to make, for example, counter circuits.
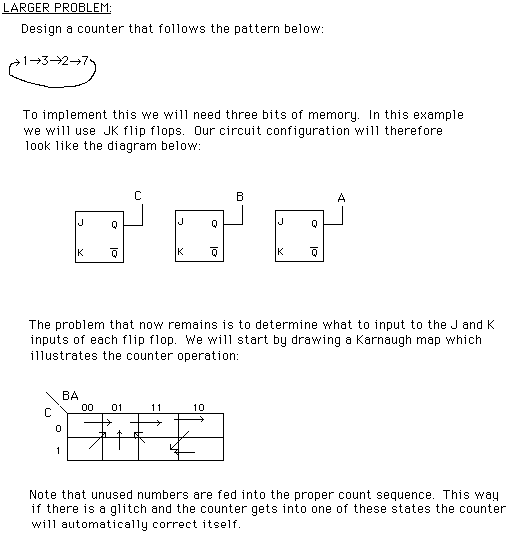
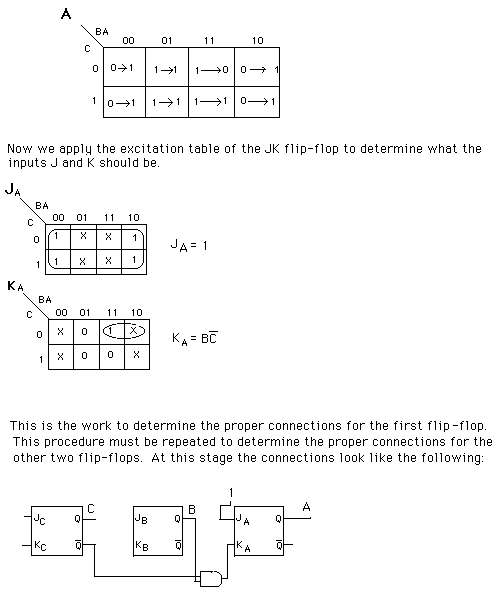
For each flip-flop we must establish what is to be connected
to the JK inputs to have that particular bit count properly.
We will look at each bit one at a time.
Here is some informattion of a JK Filp-flop for your reference.
Characteristic Table Excitation Table
========================== ===================
J K Q(t+1) Operation Q(t) Q(t+1) J K
========================== ===================
0 0 Q(t) No Change 0 0 0 x
-------------------------- -------------------
0 1 0 Reset 0 1 1 x
-------------------------- -------------------
1 0 1 Set 1 0 x 1
-------------------------- -------------------
1 1 Q'(t) Complement 1 1 x 0
========================== ===================
Conclusion
Sequential circuits are circuits that have memory.
We examined the fundamental sequential circuits like S-R flip-flops
and JK flip-flops and explained the design steps necessary
to use these as building blocks for larger sequential circuits.
Assignments
 Copyright: Department of Computer Science, University of Regina.
Copyright: Department of Computer Science, University of Regina.





